projections

If you are interested in math or maps or read this blog, you know that you cannot take the 2D surface of a sphere and conformally map it onto a plane (such that both the shape and size of the surface are depicted properly everywhere). So there are a whole lot of different projections out there. Our friend Mercator has won the popularity contest- and after all, his project is useful for most mid-latitudes, though gets a little silly near the poles (and hence, as a Canadian, is something of which I cannot help but be reminded every time I see our North so distorted).


Buckminster Fuller mapped the earth unto a 20-sided polyhedron called an isocahedron, and then unfolded it with theDymaxion map.


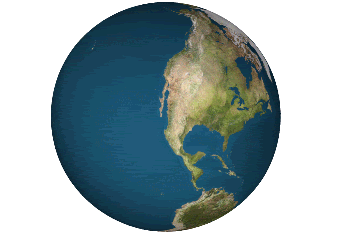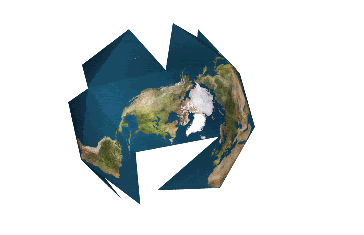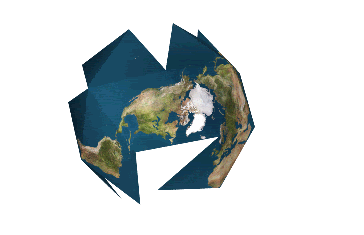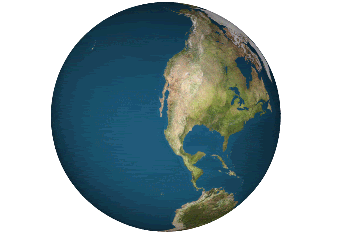
The myriahedral projection (by Jarke J. van Wijk) breaks the earth up into nearly-perfectly-mappable bits and "unfolds" them, having decided that it is better to be disjointed than wrong. This takes matter to the logical, if irregular and unexpected, extreme!





[via the map room]