Poincaré, Cubism, Non-Euclidian Geometry and Special Relativity

Cubist Poincaré, linocut, 8" x 8" by Ele Willoughby, 2022

This is a hand-printed lino block portrait in the Cubist style of mathematician Henri Poincaré. It’s one of a variable edition printed on Japanese kozo (or mulberry paper), 8” x 8” or (20.3 cm x 20.3 cm). The latest prompt for #printersolstice is Cubism.

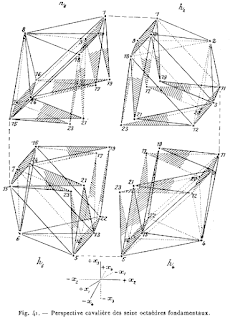
Diagram from Jouffret's 'Traité élémentaire de géométrie à quatre dimensions'

This print is about how movements in art can be connected with contemporary math and physics (and other sciences). Specifically, the way Cubism breaks from a single favoured perspective or absolute frame of reference and attempts to break down subjects into geometrical shapes from multiple points of view can be tied to advancements in non-Euclidian geometry in mathematics, special relativity (published by Einstein in 1905) and the revolution in early 20th century physics. Picasso and his circle were specifically introduced to the mathematics of the fourth dimension and Non-Euclidian geometry by his actuary and enthusiastic amateur mathematician friend Maurice Princet, who gave him the book 'Traité élémentaire de géométrie à quatre dimensions' (Elementary Treatise on the Geometry of Four Dimensions) by Esprit Jouffret, a popularization of Henri Poincaré's 'La Science et l'Hypothèse' (Science and Hypothesis). Jouffret's book includes many diagrams of four dimensional objects like hypercubes projected on the 2D surface of a page. Princet also spoke to Picasso about the work of polymath Henri Poincaré. Picasso realized that this approach to 4D geometry captured the how he wanted to depict two points of view simultaneously and art historians can trace the influence of this geometry in his earliest Cubist paintings. So I have made a Cubist style portrait of mathematician, physicist, engineer and philosopher of science Henri Poincaré (1854-1912).

Henri Poincaré 
(photograph published in 1913, via Wikipedia)

Pointcaré was called "The Last Universalist" since he excelled in such a wide range of mathematics including pure and applied math, mathematical physics and celestial mechanics. Chaos theory and the idea that deterministic systems can have sensitive dependance on initial conditions (colloquially known as the butterfly effect) seemed to explode on the scene with increasing applications in the 1980s but in fact some foundations were laid a century earlier by Poincaré. He was the first person to discover a deterministic system which exhibits chaos in the three-body problem (or how a system of  3 masses behave over under Newton's Law of Universal Gravitation). The three circular shapes in the background allude to the 3-body problem and the spiral is a hint at the chaos in the trajectories. He is considered a founder of the study of topology (how geometric properties are preserved under deformations) and stressed the importance of the invariance of physical laws under various transformations. Special relativity tells us that light speed is the universal speed limit, and that space and time are not absolute. As things approach this speed limit they experience length contraction and time dilation. We use Lorentz transformations to compare length and duration in differing frames of reference. It was Poincaré who wrote the Lorentz transformations in their modern form. He discovered the Lorentz transformations for velocity and the invariance of Maxwell's equations (for electricity, magnetism and light), which was vital part of special relativity. He published a short paper in 1905 which Einstein did not see until after he had published his own independent and revolutionary paper on special relativity. Poincaré also proposed gravitational waves, travelling at light speed from masses. It's hard to over-state his importance to 20th century math and physics.

Pablo Picasso, Portrait of Ambroise Vollard, spring of 1910 (Pushkin Museum, Moscow)

Poincaré himself worked quite intuitively and wrote, "It is only through science and art that civilization is of value."

One of the ways in which Special relativity is strange is that we discovered the problem of simultaneity. If there is no absolute frame of reference, there is no simultaneity; observers in different inertial frames of reference (that is going different speeds*) will not agree on the sequence of events or even whether two things happen at the same time. This problem of simultaneity, it can be argued, is exactly what interested Picasso, when he chose to paint two different points of view on the same canvas. This is the argument made by Miller, author of 'Einstein, Picasso: Space, Time and the Beauty That Causes Havoc' makes. Leonard Schlain, in 'Art & Physics' makes the case that Picasso in painting all sides of an object simultaneously as if he was seeing space as all here in the everlasting now, was depicting what a viewer would see astride a beam of light at the universal speed limit when time has reached its maximum dilation to the present (and only the present). 

Earlier art historians, and in fact Einstein when asked, argued that Cubism wasn't connected to relativity or non-Euclidian geometry but I think each under appreciated the other. The art historians argued the artists had no knowledge of Einstein, or Minkowski (who combined space and time into the 4D spacetime), equations or pure math. Einstein preferred earlier classical painting and argued "This new artistic 'language' has nothing in common with the Theory of Relativity" but then, he felt contemporary art and music had both degenerated. If we are less literal, I think the connection between the two movements is quite clear. There is no absolute frame of reference and both art and physics were revolutionized by this realization.

Schlain makes a further argument connecting Cubism with relativity but noting that colours also change with speed, as length contracts (including the wavelengths or colours we would observe), and colours would be merge as what is in front and behind become one. He argues we would be left with neutrals at the speed of light: white (of white light), black (of its absence),  and muddy tones of mixed colours brown and grey. These are precisely the colours Picasso and Braque used in their early Cubist paintings, and the colours of my palette for my portrait of Poincaré.

*without acceleration and/or far from large masses, so we can ignore general relativity

References

William B. Ashworth, Jr., Scientist of the Day - Esprit Jouffret, Linda Hall Library blog, March 15, 2021.

Arthur I. Miller, Henri Poincaré the unlikely like between Einstein and Picasso, The Guardian, July 17, 2021

Did Picasso know about Einstein?, Physics World, November 1, 2002

Leonard Schlain, Art & Physics, Quill William Morrow, New York, 1991

Henri Poincaré, Wikipedia, accessed January, 2022

Prints inspired by art history

I am trying to participate in the #PrinterSolstice again this year. They have created a series of prompts for each of 13 weeks starting with the (northern hemisphere) winter solstice. This year the themes are based on 20th century movements in art. It's been challenging to find time; we're once again sheltering at home and schools have gone remote here. Facilitating remote school takes a lot of my time and I cannot print at the same time, though I can plan, draw and carve. 

We started with Abstract Expressionism, which is really outside my wheelhouse, since my prints are representational. But it gave me a chance to work intuitively to create a mono print with scraps of lino.

monoprint by Ele Willoughby, 2022

Next was Art Deco. I looked at a lot of Art Deco artworks. The frequent clamshell motif and the keyhole shape in Art Nouveau works, plus seeing a number of mermaid illustrations reminded me I had long wanted to illustrate the story of Mélusine, the legendary half-fairy ancestor of the House of Lusignan and royals including the Plantagenets, whose lower half became a serpent when she bathed. She marries a nobleman but insists he must never observe her in the bath; of course he does, and she leaves him - so the keyhole shape works just right to tell the story! There are many versions, like most folklore. Sometimes she has two tails, or a fishtail or wings. There are different versions of her name and various stories are found in different regions especially France, Luxembourg and the Low Countries. I first learned of her from Manuel Mujica Láinez’s The Wandering Unicorn, which tells her story through the centuries. Her story also appears in A.S. Byatt’s Possession amongst many other places from operas to video games.

Mélusine linocut, 8" x 10" by Ele Willoughby, 2022

These art history prompts have been a challenge to link to my art practice. I've  been seeking a connection to things like science art. The third prompt was Bauhaus. In looking at Bauhaus paintings I was reminded of nothing so much as Feynman diagrams, and the exuberance action on the quantum scale, so I decided to combine quantum physics with the Bauhaus vocabulary of lines, shapes and colour palette. 

I was thinking more of the paintings of Kandinsky than the regular geometric shapes in Bauhaus design: a welter of black straight, wavy and curly lines, stripes of colour, triangles, circles and concentric rings and washes of pale colour, often on a cream coloured background. 

The Feynman diagrams are a tool of particle and quantum physics to both denote a particle interaction and also can be used to make calculations of probabilities and physical properties. Straight lines denote particles (quarks and leptons like electrons). Wavy lines denote photons. Curly lines are gluons and the dotted line is a Higgs particle. I wanted to include an electron spontaneously giving off a virtual photo and particle-antiparticle pairs, production of a Higgs particle, one diagram of the sort of we see if we smash protons together, and one hilariously named penguin diagram (in this instance producing a gluon).

Feynman Diagram Bauhaus, linocut, variable edition, 8" x 10" by Ele Willoughby, 2022

Looking at all these prints as I try to plan ahead and link them to my art practice and science art I am reminded of Leonard Shlain's book Art and Physics. It should be around here somewhere but I can't find it on my bookshelves. (Aside: this house needs a librarian.) In the book Schlain linked major movements in art with advancements in physics. I am not sure I can agree with his thesis that movements in art presaged new physics (which feels like it violates causality to me) but I greatly enjoyed the book. Others have drawn parallels between art and physics and it's clear that both math and physics were an influence of some of these major modern movements in art. In fact, this has been true for centuries; consider for instance the development of artistic perspective, or the camera obscura. One of the obvious connections is between cubism and the math of the fourth dimension and the physics of relativity. So that is something I'm thinking about for an upcoming print.

Some of the other prompts (colour field, Dadaism, Fauvism, Harlem Renaissance, Minimalism and surrealism) are less obvious for me, but I'm thinking ahead. Op Art is rather clearly related to mathematics. I have a scientific idea for Conceptual art and the seed of an idea for Pop Art. Stay tuned for more!